Background:
Superluminal tunneling (faster than light transmission of signals) was first observed at the University of Cologne with microwave photons. Soon thereafter these experiments were duplicated and validated at the University of Berkeley and Vienna. For theoretical physics the implication is that there exist spaces, devoid of time.

9th September 1999: Having met Prof. Dr. Nimtz for the first time I was shown his new tunneling experiment. As a lay person I'm not able to launch immediately into an in-depth scientific interpretation of his experiment but I will dutifully try to comprehend what I saw today, and try and share my insights and questions and make the data available as they become known.

I present here for the first time world-exclusive pictures of Prof. Nimtz's new experiment setup.  For further background information: click here

Prof. Dr. Nimtz present experiment takes it's inspiration from an experiment by Jagadis Chandra Bose, an Indian physicist born in 1858. Bose's successful public demonstration of remote signaling with radio waves in 1895 predate Marconi's experiments by two years. In 1897 Bose carried out experiments with semiconductors at frequencies as high as 60 GHz and was in the opinion of Sir Neville Mott, Nobel Laureate in 1977, at least 60 years ahead of his time.

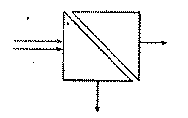
Bose's 1897 diagram of a double-prism

Modern measuring devices make it possible to investigate the effects of total reflection in more detail and to compare the results with what is known these days about quantum tunneling.

The new experiment of Prof. Nimtz explores total internal reflection of micro waves inside a dielectric prism, and the effect and characteristics of a small air gap between two identical prisms. One known effect of quantum tunneling is the propagation of photons at speeds much faster than light. The exact measure of this effect is as yet unknown in this setup. Previous tunneling experiments in different constellations have shown superluminal effects of up to 30x the speed of light.

The complete setup shows the transmitting antenna at the left, with the receiving antenna at the right.

Prof. Nimtz explaining the tunneling effect on the dielectric prism. The modulation of the microwave is approx. 1Ghz. and has a wavelength of 3cm. The gap between the prisms is 5cm, and tunneling takes place. Prof. Nimtz: "The waves enter on the left and are being reflected totally on the first wall. Only when the distance between the two prisms is not too great the can signal tunnel through the gap. It looks as if this gap here is the tunnel barrier. When we increase the gap the signal intensity received at the other end decreases. This has already been shown by Bose in 1897. But the time in which the signal traverses the tunnel has not been reliably measured until now."

The photon microwave transmitter in detail

The receiver in close-up

The monitor on the left of the setup. shows the tunneled signal arriving at the receiver on the left.

This view shows the experiment from the vantage point of the receiving antenna. Clearly visible is that the receiving antenna is connected directly with the oscilloscope.

The 7854 oscilloscope used in this demonstration. 99.999% of the emitted signal does not get tunneled.

Shown is an interruption of the microwave beam by Astrid, causing a flat line on the oscilloscope. In a working experiment setup. the prism is shielded with insulating material, to eliminate parasite waves.

Prof. Dr. Nimtz demonstrating the effects of mirroring with a metal plate. The emerging signal is reflected back into the prism where it changes the characteristics of the tunneled signal.

This is the old tunnel type used in experiments as described  in the media previously. Prof. Nimtz: "Until now we never worked with an experimental setup like the double prism. Our experiments were always confined to enclosed wave guides. It is easier to derive exact time measurements from enclosed wave guides."

Here is another tunnel design. Speeds measured on this device exceeded 9x the speed of light, within the frame of reference of this tunnel. The speed is achieved by the staggered effect of repeated change from Perspex to air.

Shown is a diagram, which appeared in a similar version in the European Physical Journal B, J.B.7,523. It illustrates the intensity of the tunneled signal versus time of a normal airborne photon moving from right to left:

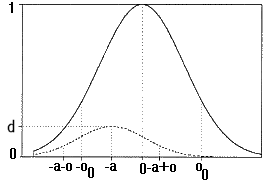
The airborne signal is shown as a solid line and the tunneled signal is shown as dots. Both fronts (waves) have traversed the same distance in the same time, with the light velocity of c. Here "d" is the maximum of the tunneled pulse, "a" is the shift of the maximum, "o" is the variance of the tunneled signal and o0 is the variance of the incoming pulse. The frequency spectrum can be infinite.

The superluminal signal does not travel back in time! Instead it arrives before the normal speed photons. The distance which the signal can theoretically traverse at superluminal speed is given by the maximum of the untunneled wave.

The velocity of the tunneled signal is measured against the velocity of a signal not being tunneled.

In the case of unlimited frequency bands the high-energy components do not tunnel in the wave-mechanical barrier. According to Nimtz these high energy components form a front which travels with the speed of light and cannot be
overtaken by the low frequency superluminal tunneling modes. The superluminal signals are shifted to earlier pulse arrival time. They overtake the front of the signal traveling at light speed and are thus not violating Einstein causality.

We cannot observe any signal moving faster than light! Nimtz explains it thus: "The analogy between the Schroedinger equation and the Helmholtz equation holds true. It is not possible to measure an evanescent mode. Obviously evanescent modes are not directly measurable in analogy to a particle in a tunnel."

What are evanescent modes? Nimtz describes these as low-frequency superluminal tunneling modes, which have a lower energy-content than the potential barrier.

Due to the large number of questions raised by this experiment I have decided to enable our readers to review the "Annalen der Physik, Leipzig, 7, (1998) 7-8, pages 618-624." I hope this article by Prof. Dr. Nimtz, which is intended to be shown here for review only, will lead to a better understanding. I am publishing the paper without alterations, so as to avoid misinterpretations and further confusion.

Click here for
"SUPERLUMINAL SIGNAL VELOCITY"
by G. Nimtz.

Acknowledgments:
I would like to thank Prof. Nimtz for taking the time to explain his experiments to me in detail
Thanks to Darrel Emerson, for the use of the Bose diagram.